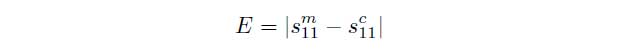Non-destructive testing
Measurement methods for material characterization
The non-destructive detection of dielectric materials using electromagnetic waves is an interesting application in science and technology. The information about the measurement object can be obtained on basis of the received signal either in transmission or reflection. The choice of measurement method and the wavelength of electromagnetic wave depend on the particular application.
The reflectometry is a measurement technique where emitted waves are reflected at discontinuities in the propagation direction. In reflection measurements the scatter fields generated on the measurement object are evaluated. The reflected waves in various directions include information about the characteristics of the measured object, such as conductivity and permittivity. Processed in a receiver the reflection points provide a picture of the environment. One example is the pulse radar tracking technology. Usually the reflection points are far away and so only the echoes from the surfaces will be evaluated.
For the transmission measurement, the attenuation of electromagnetic wave may not be too large so that the inner structure of the measurement object can be detected. The layers should have enough contrast which means different propagation properties to distinguish them from each other. Usually the evaluation of a single transmission measurement provides no depth resolution. Only several transmission measurements from different angles and the use of reconstruction algorithms allow a depth resolution of the measurement object.
The frequency selection and the measurement method depend on the application and the measurement objects. The wavelength determines the achievable resolution. Besides the limiting depth due to absorption need to be taken into account.
Reflection at non-conductive homogeneous materials
Fresnel laws
A plane wave entering from a medium with lower refractive index into an optically denser medium is reflected at the boundary surface and refracted to the surface normal. The derivation of the Fresnel laws is based on the application of Maxwell’s equations and taking into account the continuity of the tangential field components at the boundary surface. Following results can be derived:
![]()
and the Snell’s law
![]()
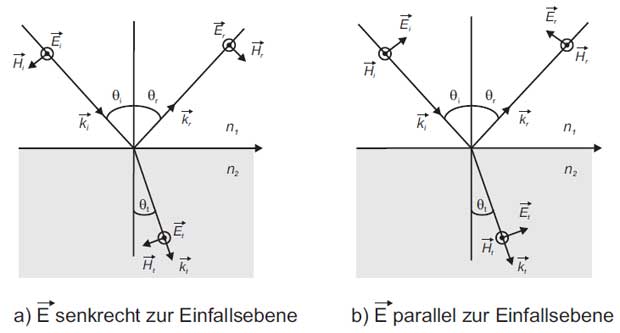
Figure 1: Reflection and refraction of a plane wave at a boundary surface
In Figure 1 two basic cases are shown. There is a distinction between vertical and parallel polarization with respect to the plane of incidence. The incidence plane is defined by the vector of propagation direction of the incident wave and the normal vector of the boundary surface.
Thus any polarization of the incident wave can be considered as the sum of two orthogonal polarization components. With the help of the Fresnel laws the distribution of the incident wave ![]() as a reflected wave
as a reflected wave ![]() and a transmitted wave
and a transmitted wave ![]() can be described. The vertical polarization will be marked as
can be described. The vertical polarization will be marked as ![]() and the parallel polarization will be marked as ||. The vertical amplitude reflection and amplitude transmission coefficient can be indicated as:
and the parallel polarization will be marked as ||. The vertical amplitude reflection and amplitude transmission coefficient can be indicated as:
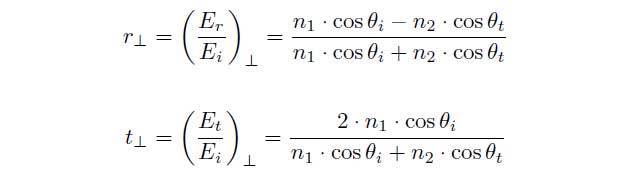
and in case of parallel polarization:
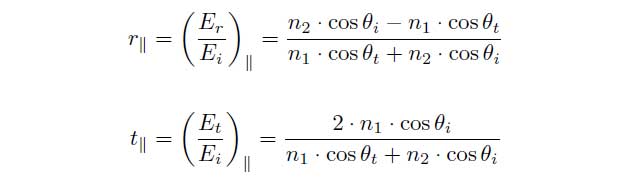
By applying Snelli’s law the equations can be simplified:
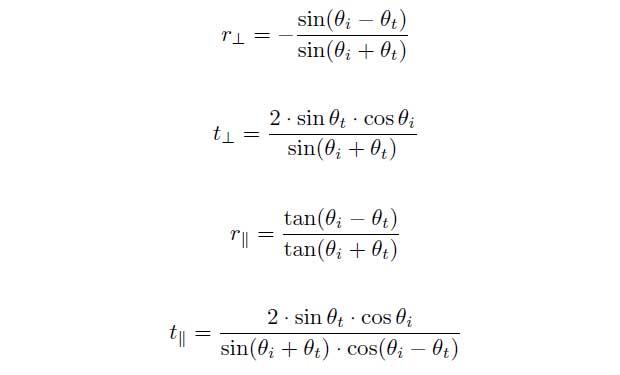
In case of normal incidence of the wave the results are independent of the polarization:
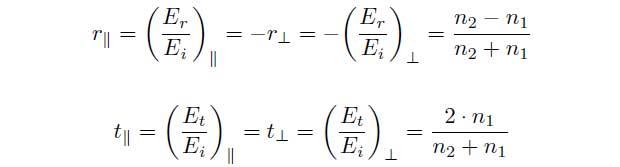
Measurement method for determining the permittivity
To determine the permittivity ![]() and the permeability
and the permeability ![]() different measurement methods have been established in practice. The material parameters are defined as follows:
different measurement methods have been established in practice. The material parameters are defined as follows:
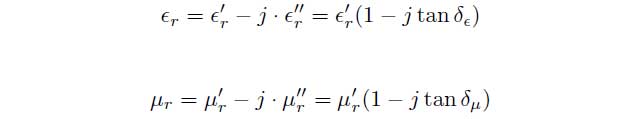
The appropriate measurement method must be selected depending on the application. In principle the measurement methods can be divided into transmission line and free-space methods:
- Probe method
- Transmission and reflection method
- Resonator method
- Free-space method
Probe method
The probe method uses a waveguide for coupling of the field into the measurement object which is carried out in either coaxial or hollow metallic waveguide. In Figure 2 various applications are presented. The measured reflection coefficient s11 can be used to determine the permittivity and loss factor of the measurement object.
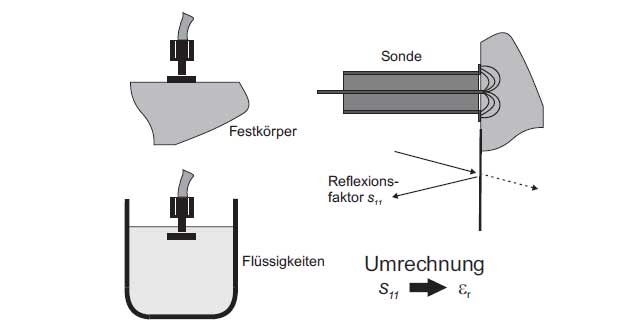
The advantages of the probe method are that it is a non-destructive process and it offers the possibility to perform a broadband measurement. In addition biological tissues and dielectric characteristics of liquids can be measured. However during the measurement of the sample it must be paid attention to the fact that there is no air gap in the contact level between the probe and the sample.
Transmission and reflection method
For the transmission and reflection method the measurement object to be examined is inserted into a hollow metallic waveguide or a coaxial line. The measurement setup is shown in Figure 3. The reflection coefficient s11 and the transmission coefficient s21 are measured using a network analyzer. The dielectric constant can be calculated from the measured values.
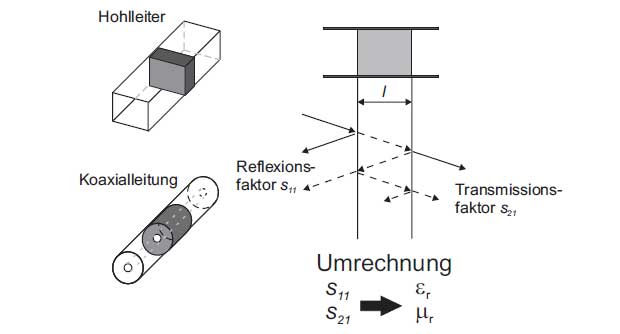
Figure 3: Transmission and reflection method for measuring the permittivity
The transmission and reflection method is suitable for a broadband characterization of the sample. But the sample preparation in coaxial technology is complex because a hollow cylinder must be manufactured. The sample preparation in waveguide technology is simple, but different waveguide geometries must be used for measurements over a wide frequency range.
Resonator method
The resonator method is based on a resonant structure with a high quality factor. The characterization is based on the fact that after insertion of the sample there is a shift in the resonant frequency. This frequency shift characterizes the permittivity ![]() . The loss factor tanδ of the material is determined due to the quality factor change. A large number of resonance structures are suitable for the resonator method. Rectangular waveguide, circular waveguide, coaxial resonators or resonators in microstrip technology are used. Another alternative is illustrated in Figure 4. It is an open resonator which is constructed with metallic mirrors. The open resonator is used primarily for measuring low-loss materials in the millimeter wave frequency range. The field distribution corresponds to that of a Gaussian beam. The diameter of the sample at the location of the beam waist should be at least six times the wavelength.
. The loss factor tanδ of the material is determined due to the quality factor change. A large number of resonance structures are suitable for the resonator method. Rectangular waveguide, circular waveguide, coaxial resonators or resonators in microstrip technology are used. Another alternative is illustrated in Figure 4. It is an open resonator which is constructed with metallic mirrors. The open resonator is used primarily for measuring low-loss materials in the millimeter wave frequency range. The field distribution corresponds to that of a Gaussian beam. The diameter of the sample at the location of the beam waist should be at least six times the wavelength.
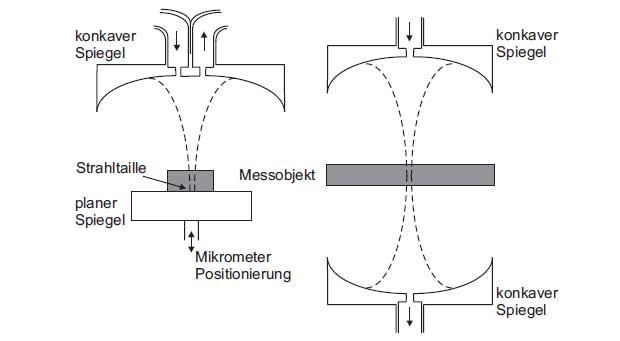
Figure 4: Resonator method for measuring the permittivity
The disadvantage of the resonance method is that the measurement takes place only at individual frequencies. The resonance structure must be adjusted accordingly for other frequency points.
Free-space method
In recent decades the free-space method has been established in the millimeter wave range for determining the permittivity  and the permeability
and the permeability ![]() . The free-space method is a non-destructive and contactless measurement method. A detailed overview of the theory of free-space methods provides Musil and ŽáÄek.
. The free-space method is a non-destructive and contactless measurement method. A detailed overview of the theory of free-space methods provides Musil and ŽáÄek.
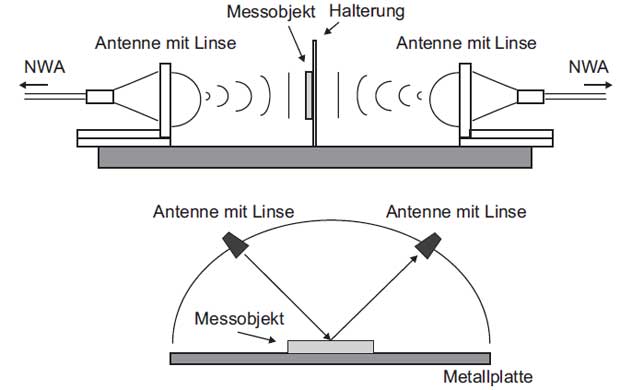
Figure 5: Free-space method for measuring the permittivity
Figure 5 shows schematically the quasi-optical transmission and reflection setup. The setups are usually made of antennas with focusing lenses because a source of error in the determination of the permittivity is diffraction effects at the edges. The sample is inserted into the beam waist of the measurement setup so the assumption of an incident plane wave is fulfilled. The advantage of the free-space method is that the manufacturing and positioning of the sample is quite simple. During the preparation of the sample it must be assured that the dimension of the sample relative to the beam waist is large so that no diffraction effects occur at the edges. In addition the sample must have planar surfaces. Another advantage is that the contactless method allows broadband tests under various external influences (e.g. temperature, humidity etc.). By mechanically moving the transmitting and receiving module the free-space method offers the possibility to create an image of the sample.
The insertion loss of the material can be determined in a simple way with the transmission measurement setup. However measurements of samples with a low loss factor represent a challenge because measuring the transmission and reflection coefficient is connected with inaccuracies and therefore no reliable loss factor results can be expected. The measurement errors are caused by multiple reflections in the system. By a suitable free-space calibration of the measurement system (TRL- or TRM-Calibration) and a filtering of the measured signal in time domain (time-domain gating) the influence of multiple reflections are reduced significantly.Therefore for samples with a low loss factor (tanδ < 0.1) a reflection setup is mainly used in which the sample is attached on a metallic reflector. The accuracy in determining the permittivity εr for the transmission setup is ±4% and for the reflection setup is ±2%.
The corresponding conversion of the measured scattering parameters into the permittivity coefficient in case of the transmission setup is:
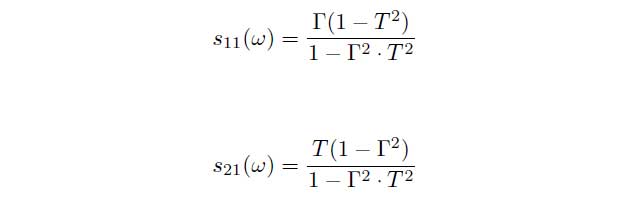
with the transmission coefficient T and the reflection coefficient Γ
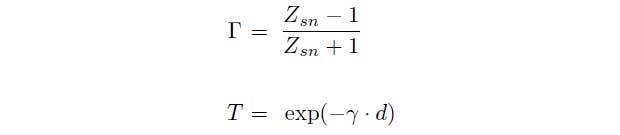
Zsn is the normalized impedance of the material and γ denotes the propagation coefficient of the material. These parameters can be linked with the permittivity εr and the permeability ![]() by the following equations.
by the following equations.
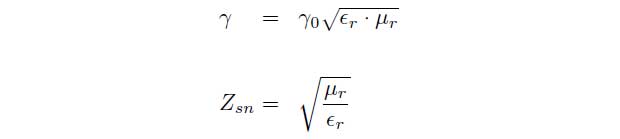
γ0 = j · 2π/λ0 represents the propagation coefficient of free space. T and Γ can also be determined depending on the measured scattering parameters.
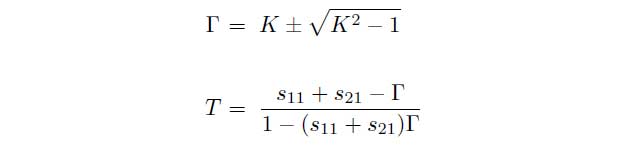
with
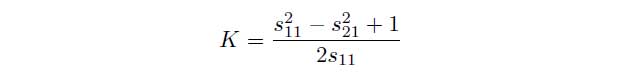
Thus it is possible to determine the material parameters for the transmission setup:
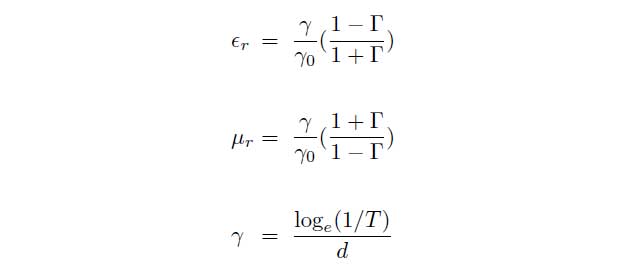
In case of the reflection setup the following system of equations can be used to determine the permittivity εr:
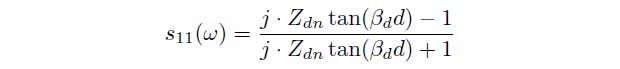
Zdn is the normalized impedance of the material and d is the thickness of the material. To determine the permittivity εr of non-magnetic materials the measurement values are associated with the following equations.
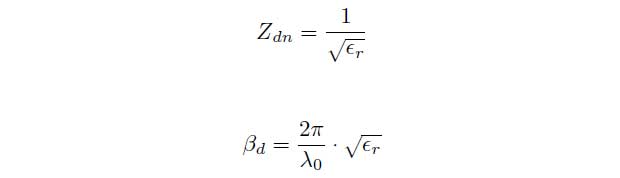
Because the equations cannot explicitly be solved for the parameters s11(ω) and d the permittivity εr have to be determined iteratively. As an indicator an error function E is used which is defined as the difference between the measured and calculated scattering parameters (sm11, sc11). The goal is to minimize the error function E.